Row and Column Major Ordering in an Array

/ Data Structures & Algorithms (DSA) / By

Row and Column Major Ordering in an Array defines how multi-dimensional arrays are stored in memory. These ordering methods affect memory access patterns, performance, and how efficiently programs execute. Whether you’re a C/C++ developer, data scientist, or systems engineer, understanding these storage techniques is essential for writing high-performance code.

What is Row-Major Order?

In row-major order, elements of a 2D array are stored row by row in contiguous memory locations. This layout is common in languages like C, C++, Java, and Python (NumPy).

Key Characteristics of Row-Major Order

  • Stores the entire first row first, then the second, and so on.
  • Row elements are adjacent in memory, improving row-wise access speed.
  • Ideal for operations like row-wise traversals or image processing.

Example:

For a 3×3 matrix:

1 2 3
4 5 6
7 8 9

Row-major layout in memory:
[1, 2, 3, 4, 5, 6, 7, 8, 9]

row major order in an Array

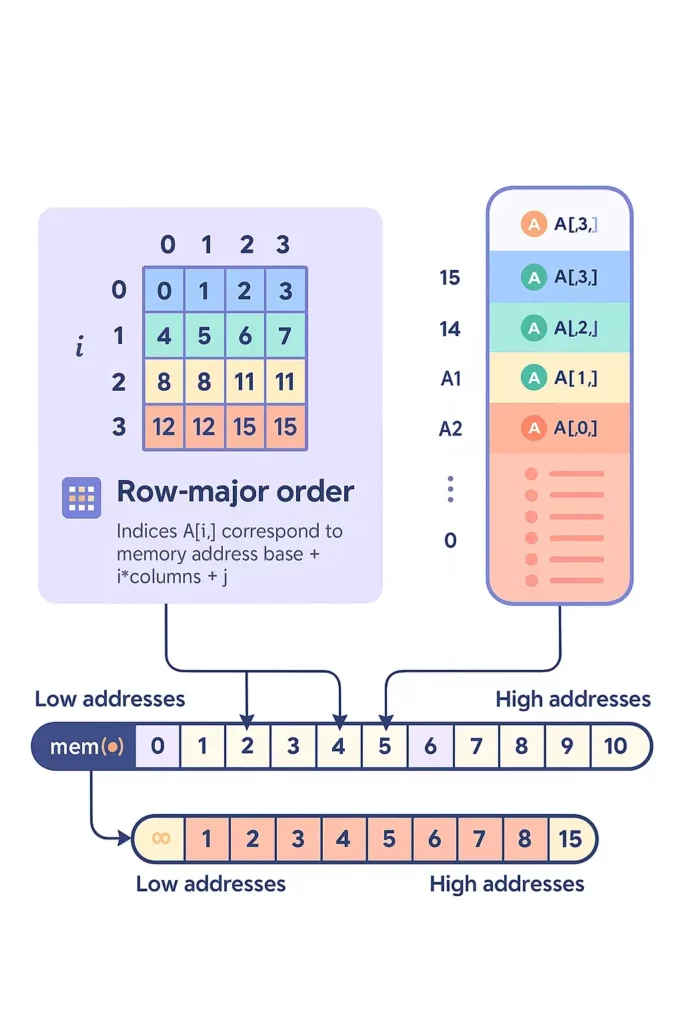
Calculating Addresses in Row-Major Order

To compute the memory address of an element A[i][j] in row-major:

Address = Base + W * (C * i + j)

Where:

  • Base = Starting memory address
  • W = Word size (bytes per element)
  • C = Number of columns
  • i = Row index
  • j = Column index

This formula is key for understanding how arrays are accessed internally in memory during execution.

What is Column-Major Order?

In column-major order, array elements are stored column by column. This method is default in languages like Fortran, MATLAB, and some linear algebra libraries like BLAS.

Key Characteristics of Column-Major Order

  • Stores all elements of the first column, then the second, and so on.
  • Column elements are stored contiguously.
  • Beneficial for column-wise operations in scientific computing.

Example:

For the same 3×3 matrix:

1 2 3
4 5 6
7 8 9

Column-major layout in memory:
[1, 4, 7, 2, 5, 8, 3, 6, 9]

Column major order in an Array

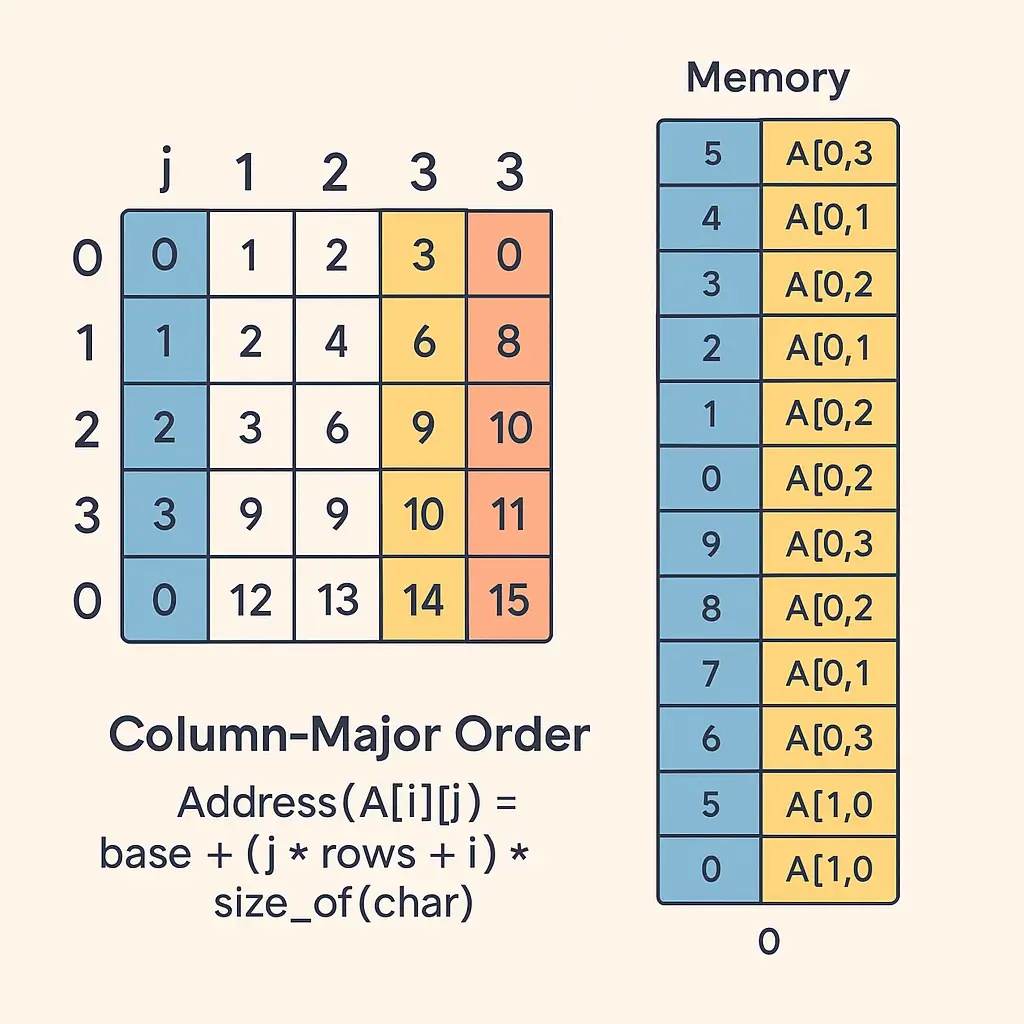
Calculating Addresses in Column-Major Order

To compute the address of A[i][j] in column-major:

Address = Base + W * (R * j + i)

Where:

  • Base = Starting address
  • W = Word size
  • R = Number of rows
  • i = Row index
  • j = Column index

This layout benefits column-based mathematical operations and improves performance for certain matrix calculations.

Row and Column Major Ordering in an Array: Why It Matters

1. Performance Optimization

Correct memory access patterns (e.g., row-wise in row-major) ensure data is fetched efficiently, reducing cache misses and boosting speed.

2. Language and Library Compatibility

Misunderstanding default ordering can lead to bugs when using libraries like OpenCV (row-major) or MATLAB (column-major).

Choosing the Right Memory Ordering

1. Based on Programming Language

  • Row-Major: C, C++, Java, Python (NumPy default)
  • Column-Major: Fortran, MATLAB, R

2. Based on Application

  • Use row-major for horizontal scanning (e.g., images, tables).
  • Use column-major for matrix operations and scientific calculations.

Row and Column Major Ordering: Real-World Applications

Image Processing

Pixel data in images are stored row-wise. Accessing them row by row (in row-major systems) improves efficiency and readability.

Matrix Multiplication

In numerical computing, column-major ordering provides better performance when accessing matrix columns repeatedly.

Visualizing the Memory Layout

Row-Major Example (3×3 Matrix)

Memory: [A[0][0], A[0][1], A[0][2], A[1][0], A[1][1], A[1][2], A[2][0], A[2][1], A[2][2]]

Column-Major Example (3×3 Matrix)

Memory: [A[0][0], A[1][0], A[2][0], A[0][1], A[1][1], A[2][1], A[0][2], A[1][2], A[2][2]]

Visual clarity helps in debugging and optimizing loops in low-level programming.

Library/LanguageDefault OrderNotes
C / C++Row-MajorManual memory optimization supported
NumPy (Python)Row-MajorUse order='F' for column-major
MATLABColumn-MajorNative to scientific computing
FortranColumn-MajorOptimized for numerical tasks
OpenCVRow-MajorUsed in image and video processing

Tips for Optimizing Code Based on Memory Order

  • Use loop ordering that matches your memory layout to improve CPU cache usage.
  • When working with NumPy or similar, choose order='C' or order='F' explicitly.
  • In GPU programming (e.g., CUDA), understanding memory layout avoids performance bottlenecks.

Frequently Asked Questions: Row and Column Major Ordering in an Array

Q1. Which is more common, row-major or column-major?

Row-major is more commonly used, especially in languages like C, C++, and Python. Column-major is typical in MATLAB and Fortran.

Q2. Can I control the ordering of arrays?

Yes. In some libraries like NumPy, you can define array ordering using order='C' for row-major or order='F' for column-major.

Q3. Does ordering affect performance?

Absolutely. Using the wrong access pattern for your layout can cause cache misses and slow down your code.

Q4. Can I switch between orders in code?

Yes, many libraries allow transposing or copying arrays to switch between orders, but it may involve additional memory overhead.

Q5. How do I remember the formulas?

Row-Major: C * i + j
Column-Major: R * j + i
Just remember: rows come first in row-major; columns come first in column-major.

Conclusion: Mastering Row and Column Major Ordering in an Array

Understanding Row and Column Major Ordering in an Array is essential for optimizing memory access and building high-performance applications. Whether working in data science, embedded systems, or scientific computing, this knowledge ensures your arrays are accessed efficiently, leading to better speed and reduced resource consumption.

Always align your code logic with the array’s memory layout for optimal results—and never overlook how your data is stored under the hood.

Related Posts

Scroll to Top