Imagine a stack of plates: you can only add or remove a plate from the top. This Last-In, First-Out (LIFO) principle is the foundation of the stack data structure in computer science. While simple in concept, stacks play a crucial role in numerous applications, from managing function calls in your code to powering the back button in your web browser. Let’s dive into the world of stacks, their operations, and their wide-ranging applications.
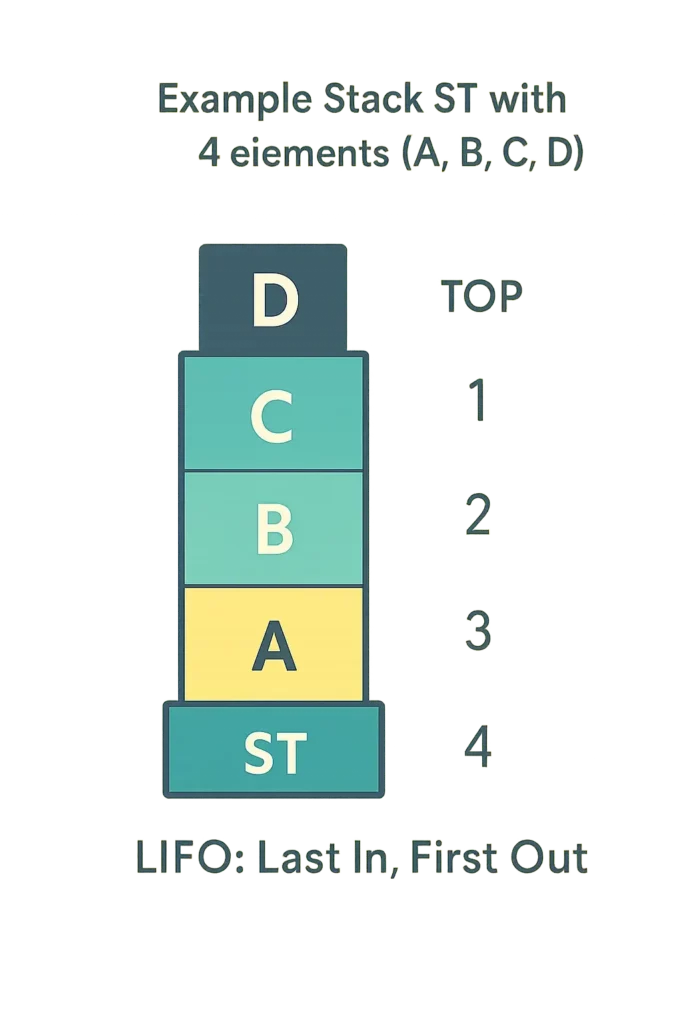
Understanding Stacks: The LIFO Principle in Action
A stack is a linear collection of elements where items are added (pushed) and removed (popped) from the same end, known as the top. This LIFO behavior makes stacks ideal for scenarios where the most recently added item is the first one needed.
Core Stack Operations
- Push: Adds an element to the top of the stack.
- Pop: Removes and returns the top element from the stack.
- Peek: Retrieves the value of the top element without removing it.
- isEmpty: Checks if the stack is empty.
- isFull: Checks if the stack is full (applicable for fixed-size stacks).
Applications of Stacks: Beyond the Kitchen
Stacks may seem simple, but their applications are surprisingly diverse:
- Function Calls:
- When a program calls a function, the return address (where the program should resume after the function finishes) is pushed onto a stack.
- Local variables and parameters of the function are also pushed onto the stack.
- When the function completes, the return address is popped from the stack, and the program continues from where it left off.
- Expression Evaluation:
- Stacks are used to evaluate arithmetic expressions, especially in postfix (Reverse Polish Notation) form.
- Operands are pushed onto the stack, and operators are applied to the top elements of the stack.
- Undo/Redo Functionality:
- Applications like text editors and photo editors use stacks to keep track of actions, allowing users to undo or redo their steps.
- Browser History:
- Web browsers maintain a stack of visited web pages, enabling users to navigate back and forth using the back and forward buttons.
- Memory Management:
- Operating systems use stacks to manage the allocation and deallocation of memory for processes and function calls.
- Recursion:
- Recursive functions (functions that call themselves) rely heavily on stacks to keep track of each recursive call’s state.
- Backtracking Algorithms:
- Stacks are used in algorithms like depth-first search to explore and backtrack through decision paths.
- Syntax Checking and Parsing:
- Compilers use stacks to check for balanced parentheses and other syntactic structures in code.
Implementing Stacks
Stacks can be implemented using either arrays or linked lists.
- Array Implementation: Simple and efficient for fixed-size stacks.
- Linked List Implementation: More flexible for dynamic resizing.
The choice depends on the specific requirements of your application.
FAQs: Stack and application of stack
Q: Why is the LIFO principle important for stacks?
A: The LIFO principle ensures that operations are performed on the most recently added data, which is often necessary in function calls and expression evaluation.
Q: What happens if I try to pop an element from an empty stack?
A: This results in a stack underflow error, as there’s no element to remove.
Q: How does a stack differ from a queue?
A: While stacks follow LIFO, queues follow FIFO (First-In, First-Out), like a line of people.
Q: Are there any real-world examples of stacks outside of computing?
A: Yes! Think of a stack of books, a pile of laundry, or even the way you put on and take off clothes—these are all examples of the LIFO principle in action.
Q: Can I have multiple stacks in a program?
A: Absolutely! You can create and manage multiple stacks to handle different tasks or data within your program.